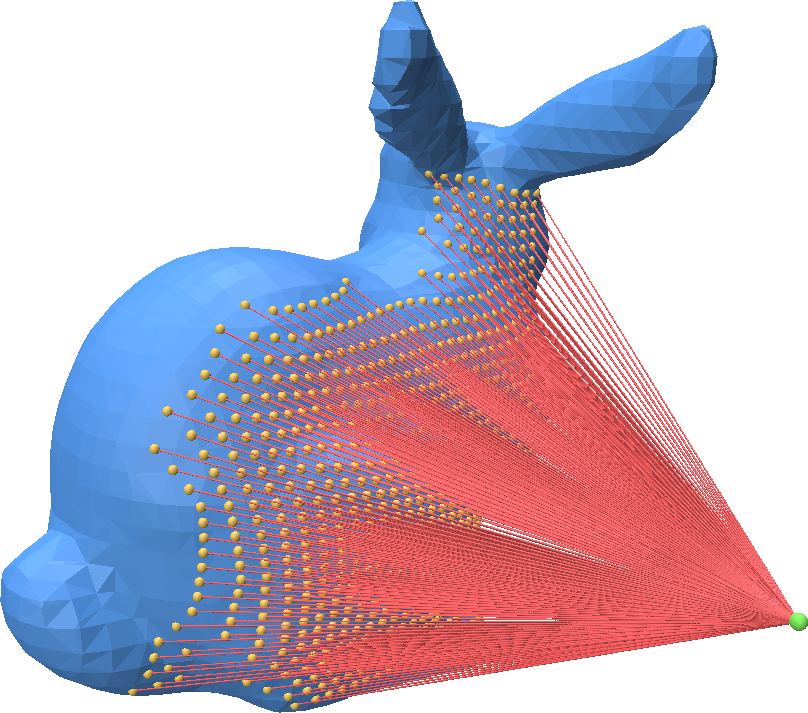
Ray Mesh Intersection

Point-Cloud-Utils supports fast ray-mesh intersection using Intel Embree. There are two ways of performing ray-mesh queries. For one-off queries, use the functional interface, and for repeated queries on a mesh, use RayMeshIntersector

One-off Ray-Mesh Queries using the Functional Interface

You can call ray_mesh_intersection to compute the intersection between a collection of rays and a triangle mesh:

import point_cloud_utils as pcu
import numpy as np

v, f = pcu.load_mesh_vf("bunny.ply")

# Generate a raster grid of Rays looking down the +Z axis
x, y = np.mgrid[-0.5:0.5:32j, -0.5:0.5:32j]
ray_d = np.stack([x.flatten(), y.flatten(), np.ones_like(x.flatten())], axis=-1)
ray_d /= np.linalg.norm(ray_d, axis=-1, keepdims=True)  # Normalize ray directions -- shape [N, 3]

# Rays originating at -Z looking down the Z-axis
ray_o = np.array([0.0, 0.15, -0.75])  
ray_o = np.repeat(ray_o[None, :], ray_d.shape[0], axis=0)  # Repeat the ray origin so there is one per ray -- shape [N, 3]

fid, bc, t = pcu.ray_mesh_intersection(v.astype(ray_o.dtype), f, ray_o, ray_d)

# True only at the rays which intersected the shape
hit_mask = fid >= 0

ray_intersections = pcu.pcu.interpolate_barycentric_coords(f, fid[hit_mask], bc[hit_mask], v)

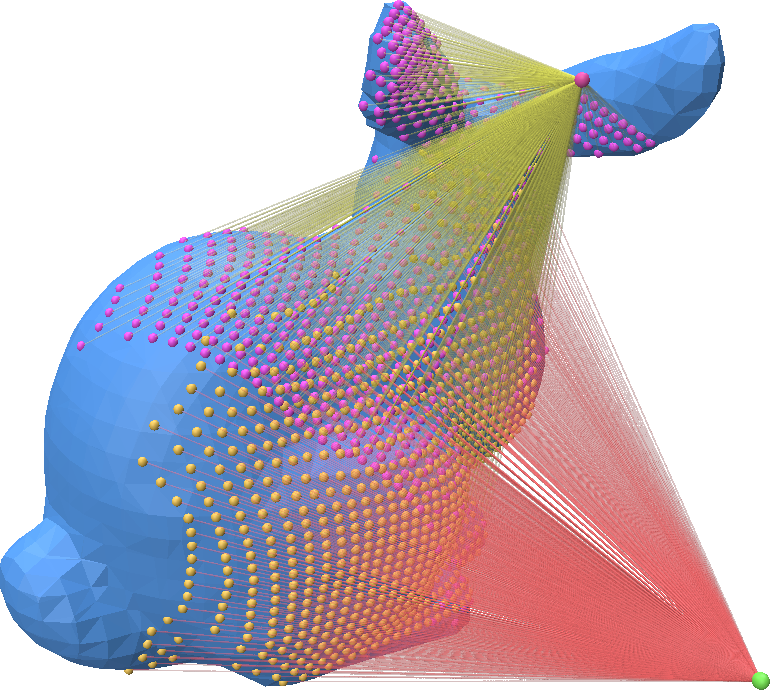
Ray-mesh intersection

Computing one-off ray-mesh intersection queries.

Repeated Ray-Mesh Queries using RayMeshIntersector

You can call ray_mesh_intersection to compute the intersection between a collection of rays and a triangle mesh:

import point_cloud_utils as pcu
import numpy as np

v, f = pcu.load_mesh_vf("bunny.ply")

# Generate a raster grid of Rays looking down the +Z axis
x, y = np.mgrid[-0.5:0.5:32j, -0.5:0.5:32j]
ray_d = np.stack([x.flatten(), y.flatten(), np.ones_like(x.flatten())], axis=-1)
ray_d /= np.linalg.norm(ray_d, axis=-1, keepdims=True)  # Normalize ray directions -- shape [N, 3]

# Rays originating at -Z looking down the Z-axis
ray_o = np.array([0.0, 0.15, -0.75])  
ray_o = np.repeat(ray_o[None, :], ray_d.shape[0], axis=0)  # Repeat the ray origin so there is one per ray -- shape [N, 3]

# Generate new rays via a random rotation
random_rotation = np.linalg.svd(np.random.randn(3, 3))[0]
ray_o2 = np.ascontiguousarray((random_rotation @ ray_o.T).T)
ray_d2 = np.ascontiguousarray((random_rotation @ ray_d.T).T)

intersector = pcu.RayMeshIntersector(v, f)

# Intersect first batch of rays
fid, bc, t = intersector.intersect_rays(ray_o, ray_d)
hit_mask = fid >= 0  # True only at the rays which intersected the shape
ray_intersections = pcu.interpolate_barycentric_coords(f, fid[hit_mask], bc[hit_mask], v)

# Intersect second batch of rays
fid2, bc2, t2 = intersector.intersect_rays(ray_o2, ray_d2)
hit_mask2 = fid >= 0  # True only at the rays which intersected the shape
ray_intersections2 = pcu.interpolate_barycentric_coords(f, fid2[hit_mask2], bc2[hit_mask2], v)

Ray-mesh intersection

Computing repeated ray-mesh intersections using `RayMeshIntersector`. Each seperate batch of rays is colored differently.

Representing mesh-surface samples in Point Cloud Utils

Point Cloud Utils returns samples on the surface of a mesh using Barycentric Coordinates. i.e. each sample is encoded as:

  1. The index of the mesh face containing it (usually referred to as fid)
  2. The barycentric coordinates of the point within that face (usually referred to as bc)

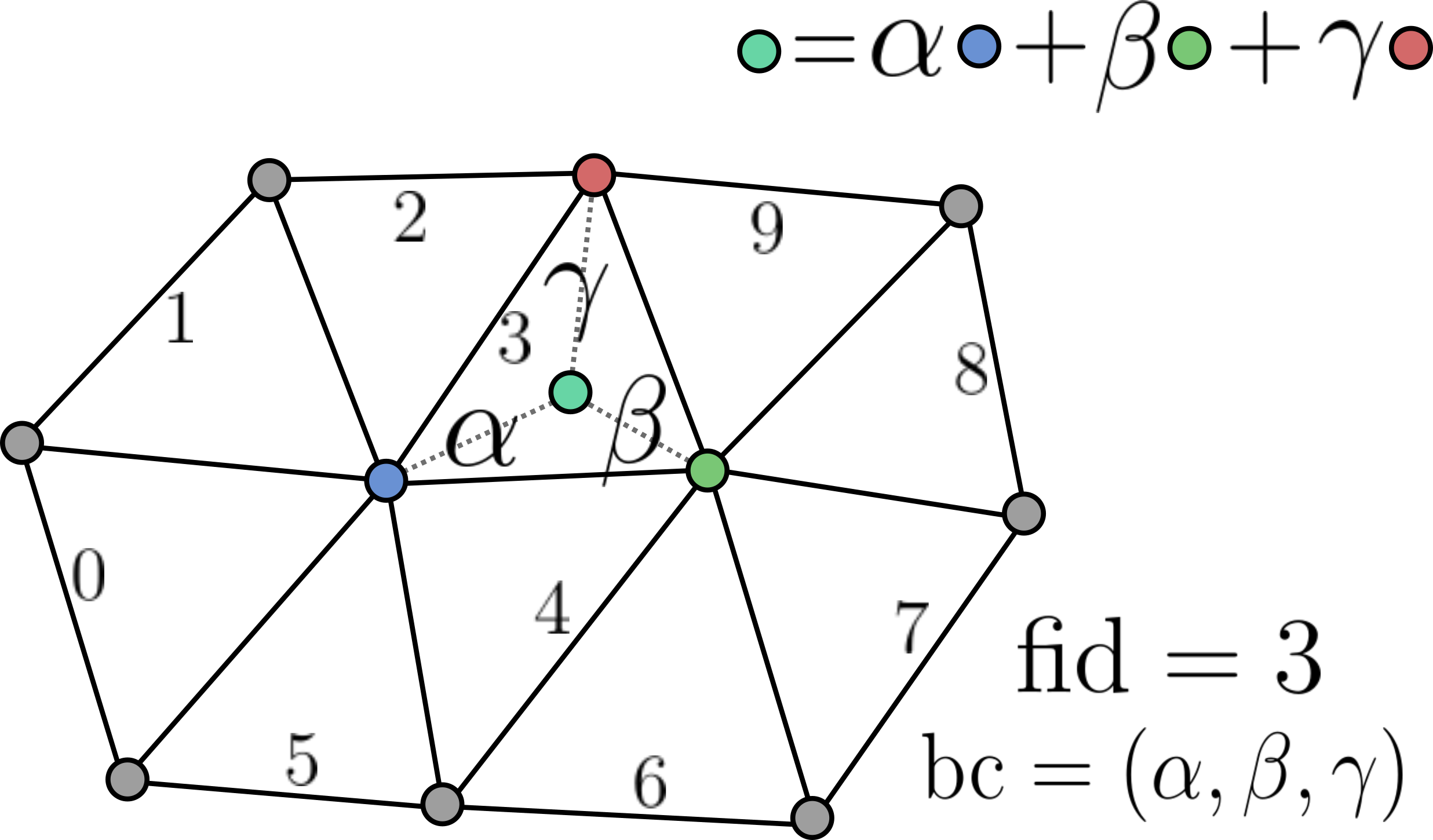
Barycentric coordinates illustration

Encoding surface samples as barycentric coordinates. The teal point is the barycentric combination with weights \((\alpha, \beta, \gamma)\) in face 3.

The reason for encoding points in this way is that it allows us to interpolate any quantity stored at the vertices (including their positions) of a mesh to the sample positions, and thus sample vertex attributes.

To recover vertex quantities from fid, bc pairs use the function pcu.interpolate_barycentric_coords(f, fid, bc, vertex_quantity)