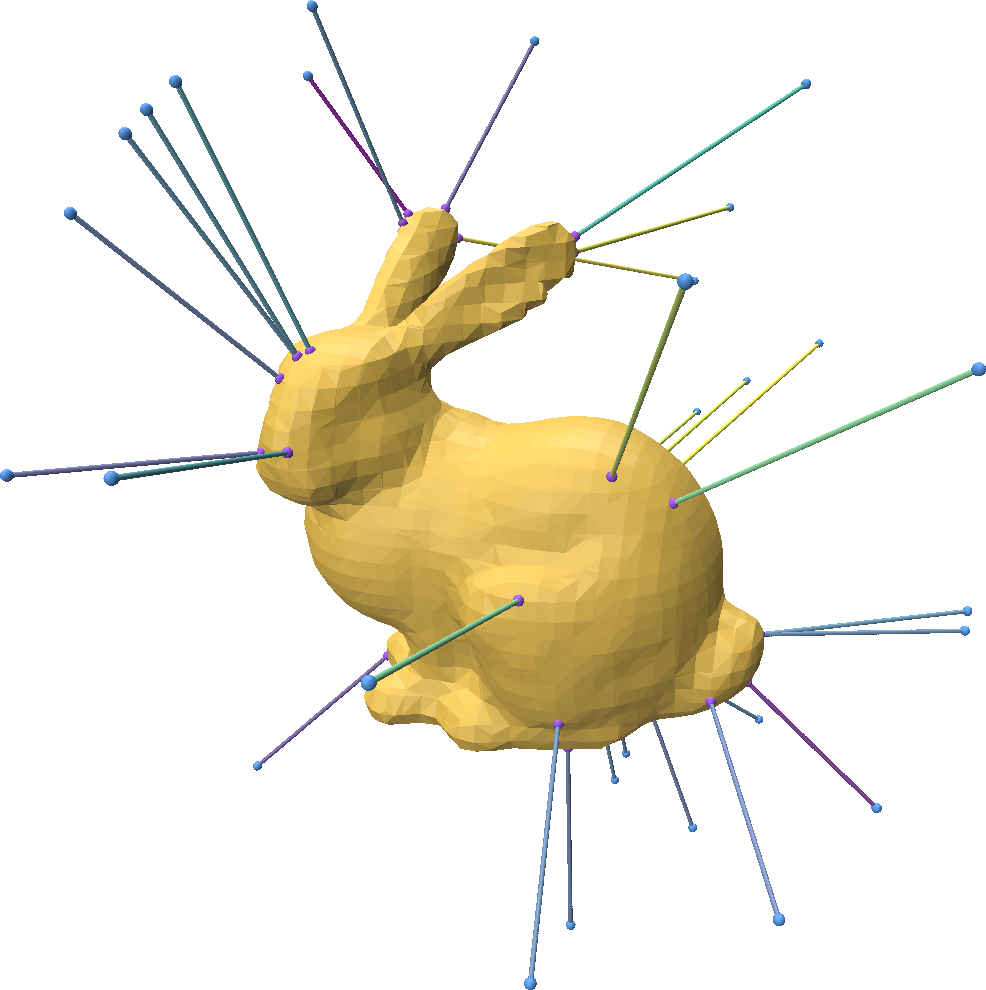
Finding Closest Points Between Point Clouds and Meshes

You can easily find the closest point on a mesh to any 3D point in space with Point-Cloud-Utils.

import point_cloud_utils as pcu
# Load a mesh stored in my_mesh.ply:
#   v is a NumPy array of coordinates with shape (V, 3)
#   f is a NumPy array of face indices with shape (F, 3)
v, f = pcu.load_mesh_vf("bunny.ply")

# Generate random points on a sphere around the shape
p = np.random.randn(33, 3)
p /= np.linalg.norm(p, axis=-1, keepdims=True)

# Compute the shortest distance between each point in p and the mesh:
#   dists is a NumPy array of shape (P,) where dists[i] is the
#   shortest distnace between the point p[i, :] and the mesh (v, f)
dists, fid, bc = pcu.closest_points_on_mesh(p, v, f)

# Interpolate the barycentric coordinates to get the coordinates of 
# the closest points on the mesh to each point in p
closest_pts = pcu.interpolate_barycentric_coords(f, fid, bc, v)

Closest points on a mesh

The nearest neighbors (purple dots) on the mesh to the blue points. The edges connect each point to its nearest point.

Representing mesh-surface samples in Point Cloud Utils

Point Cloud Utils returns samples on the surface of a mesh using Barycentric Coordinates. i.e. each sample is encoded as:

  1. The index of the mesh face containing it (usually referred to as fid)
  2. The barycentric coordinates of the point within that face (usually referred to as bc)

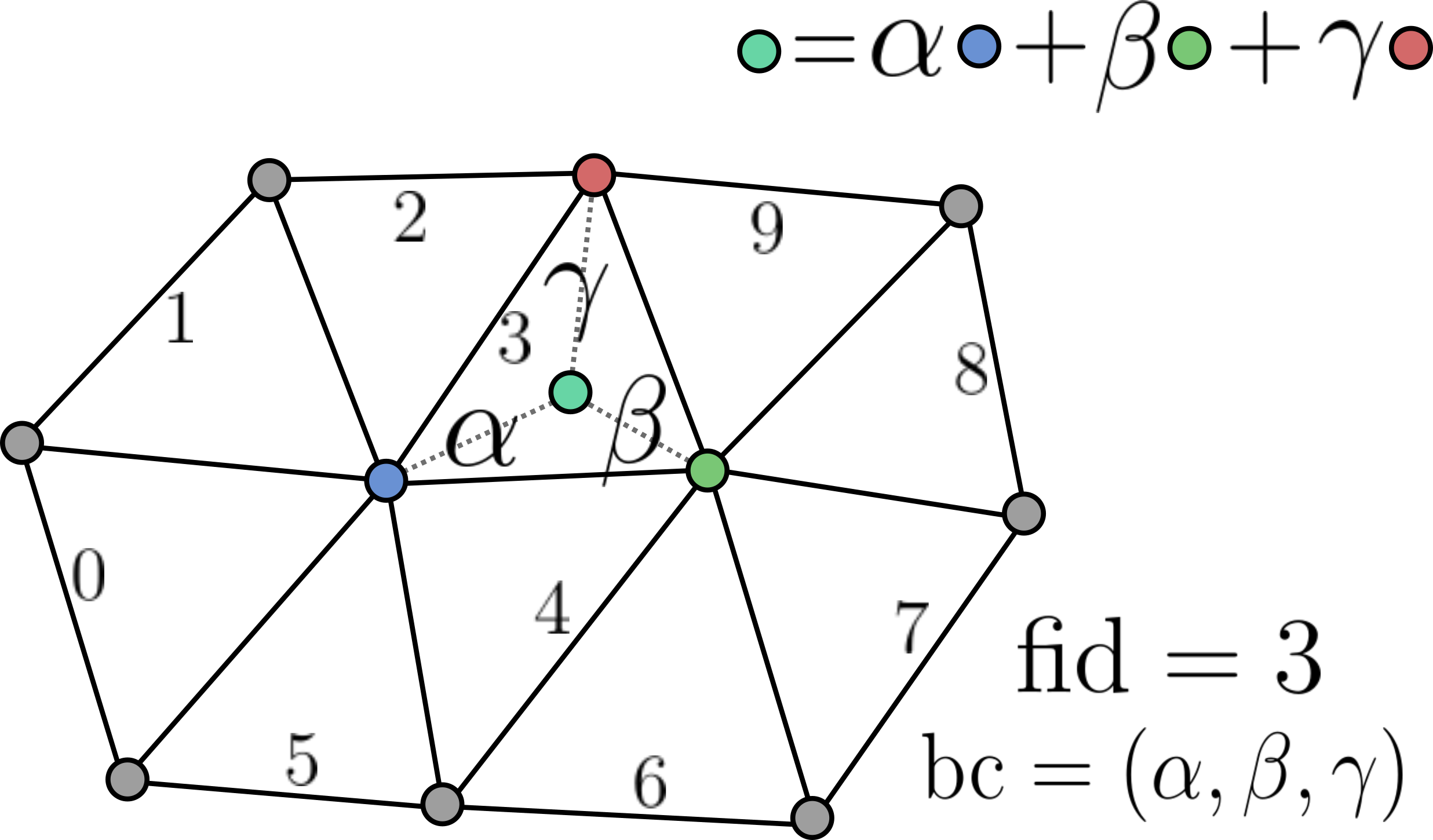
Barycentric coordinates illustration

Encoding surface samples as barycentric coordinates. The teal point is the barycentric combination with weights \((\alpha, \beta, \gamma)\) in face 3.

The reason for encoding points in this way is that it allows us to interpolate any quantity stored at the vertices (including their positions) of a mesh to the sample positions, and thus sample vertex attributes.

To recover vertex quantities from fid, bc pairs use the function pcu.interpolate_barycentric_coords(f, fid, bc, vertex_quantity)