Computing Signed Distances (SDFs) to Meshes
Many applications require a signed distance function (SDF) representation for a 3D shape. For example, many shape reconstruction neural networks such as DeepSDF require such a representation for training. Unfortunately, most 3D shape data is stored as a triangle mesh, making SDFs not readily available. Point-Cloud-Utils makes it very easy to extract signed distances from a triangle mesh.
Remark about mesh quality
To extract an SDF for a triangle mesh, the mesh must be of relatively good quality (manifold, watertight, no sliver triangles, etc...). To clean up a mesh for SDF extraction see Making a triangle mesh watertight.
SDF Overview
A signed distance function \(f : \mathbb{R}^3 \rightarrow \mathbb{R}\) maps 3D points \(x \in \mathbb{R}^3\) to the nearest distance between \(x\) and some surface \(S\). In other words: $$ f(x) = \min_{x' \in S} |x - x'|_2 $$ The zero level set of the SDF \(f\) are precisely the set of points which lie on the surface. i.e. $$ S = {x : f(x) = 0} $$ The image below shows a plot of the SDF for the boundary of the letters PCU.

Computing an SDF to a Mesh
We can compute the signed distance of a set of points in Point-Cloud-Utils in the following way:
import numpy as np
import point_cloud_utils as pcu
# 1000 random query points to compute the SDF at
query_pts = np.random.rand(1000, 3)
v, f = pcu.load_mesh_vf("bunny.ply")
# sdf is the signed distance for each query point
# fid is the nearest face to each query point on the mesh
# bc are the barycentric coordinates of the nearest point to each query point within the face
sdf, fid, bc = pcu.signed_distance_to_mesh(query_pts, v, f)
Below we plot the sampled points colored by their SDF values:
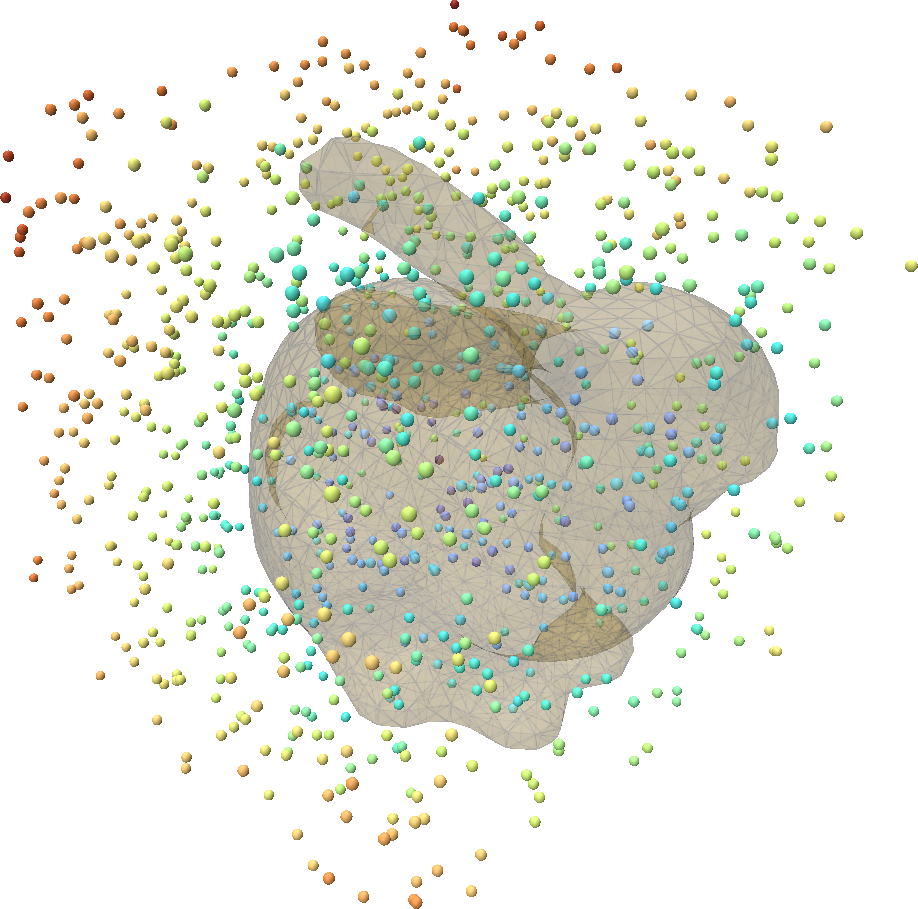
Representing mesh-surface samples in Point Cloud Utils
Point Cloud Utils returns samples on the surface of a mesh using Barycentric Coordinates. i.e. each sample is encoded as:
- The index of the mesh face containing it (usually referred to as
fid) - The barycentric coordinates of the point within that face (usually referred to as
bc)
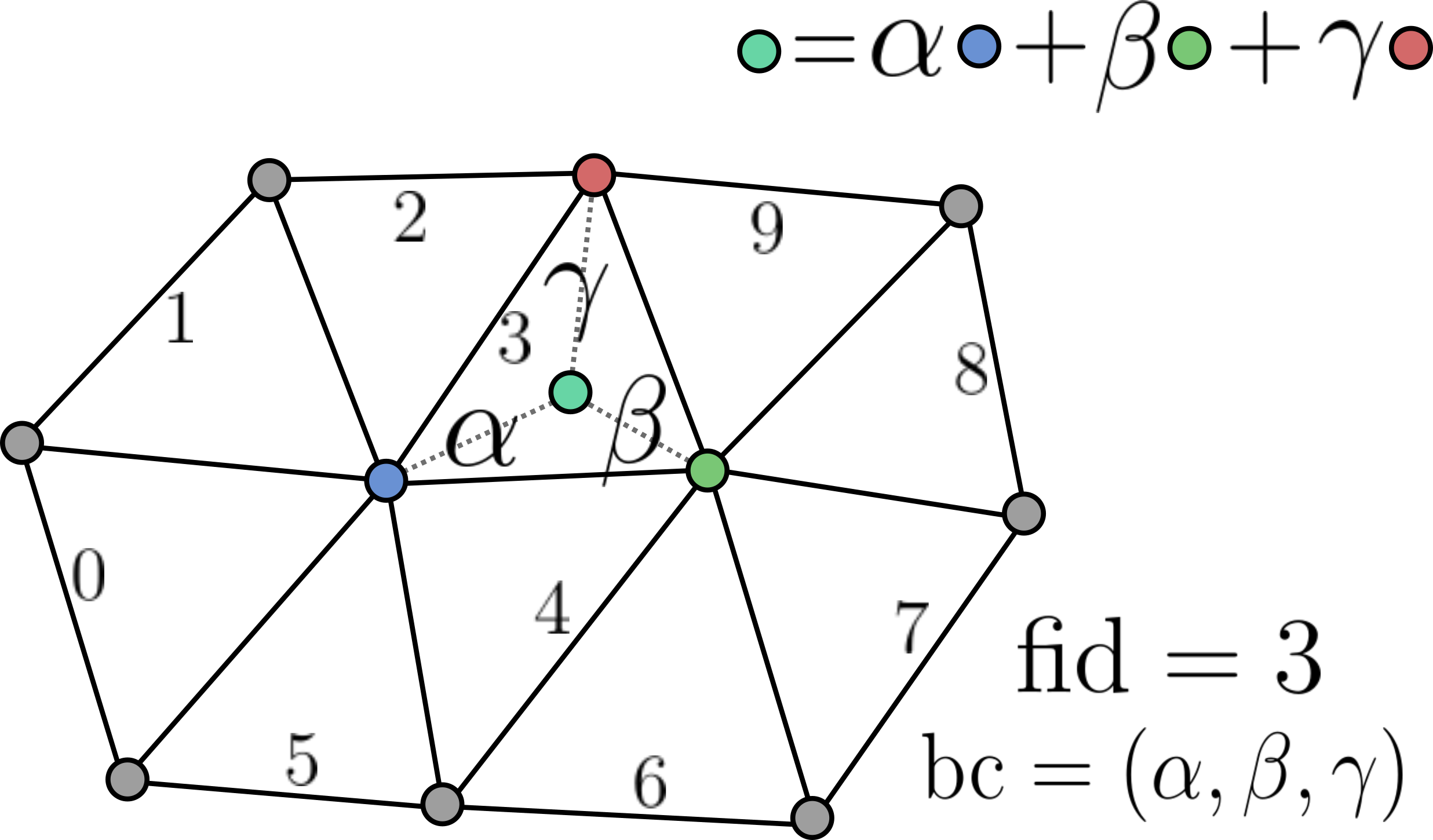
To recover vertex quantities from fid, bc pairs use the function pcu.interpolate_barycentric_coords(f, fid, bc, vertex_quantity)