XCube: Large-Scale 3D Generative Modeling using Sparse Voxel Hierarchies
Xuanchi Ren, Jiahui Huang, Xiaohui Zeng, Ken Museth, Sanja Fidler, Francis Williams
arXiv 2023
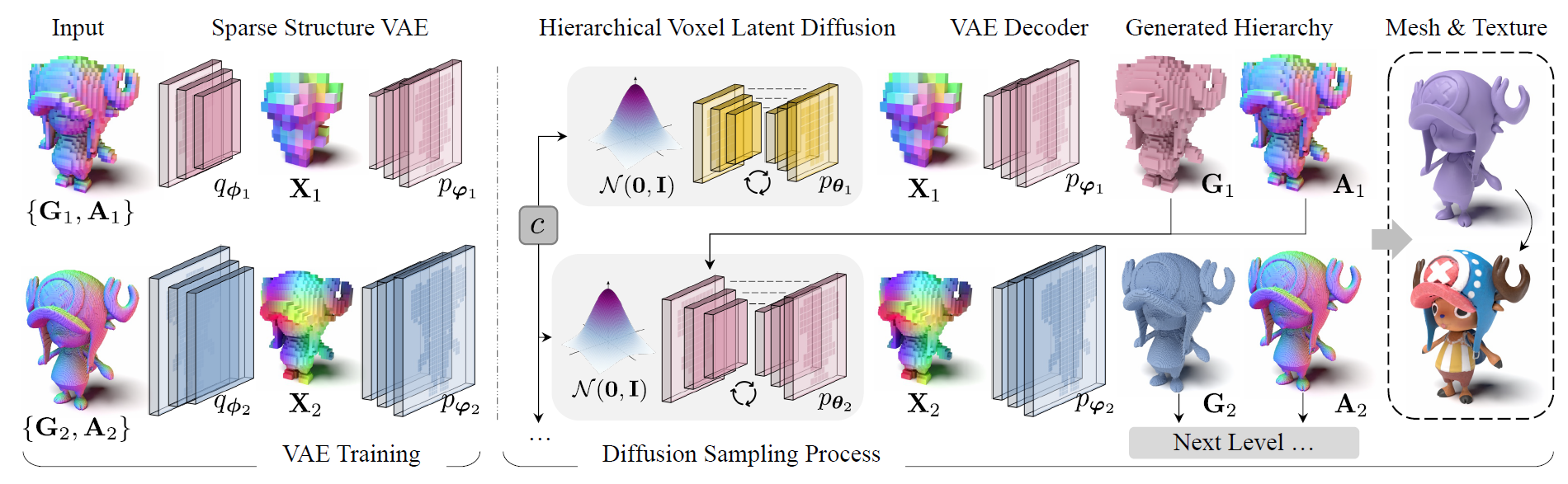
We present XCube, a novel generative model for high-resolution sparse 3D voxel grids with arbitrary attributes. Our model can generate millions of voxels with a finest effective resolution of up to 10243 in a feed-forward fashion without time-consuming test-time optimization. To achieve this, we employ a hierarchical voxel latent diffusion model which generates progressively higher resolution grids in a coarse-to-fine manner using a custom framework built on the highly efficient VDB data structure. Apart from generating high-resolution objects, we demonstrate the effectiveness of XCube on large outdoor scenes at scales of 100m×100m with a voxel size as small as 10cm. We observe clear qualitative and quantitative improvements over past approaches. In addition to unconditional generation, we show that our model can be used to solve a variety of tasks such as user-guided editing, scene completion from a single scan, and text-to-3D.
Neural LiDAR Fields for Novel View Synthesis
Shengyu Huang, Zan Gojcic, Zian Wang, Francis Williams, Yoni Kasten, Sanja Fidler, Konrad Schindler, Or Litany
ICCV 2023
The reconstruction of a discrete surface from a point cloud is a fundamental geometry processing problem that has been studied for decades, with many methods developed. We propose the use of a deep neural network as a geometric prior for surface reconstruction. Specifically, we overfit a neural network representing a local chart parameterization to part of an input point cloud using the Wasserstein distance as a measure of approximation. By jointly fitting many such networks to overlapping parts of the point cloud, while enforcing a consistency condition, we compute a manifold atlas. By sampling this atlas, we can produce a dense reconstruction of the surface approximating the input cloud. The entire procedure does not require any training data or explicit regularization, yet, we show that it is able to perform remarkably well: not introducing typical overfitting artifacts, and approximating sharp features closely at the same time. We experimentally show that this geometric prior produces good results for both man-made objects containing sharp features and smoother organic objects, as well as noisy inputs. We compare our method with a number of well-known reconstruction methods on a standard surface reconstruction benchmark.
Neural Kernel Surface Reconstruction
Jiahui Huang, Zan Gojcic, Matan Atzmon, Or Litany, Sanja Fidler, Francis Williams
CVPR 2023 (Highlight Paper)
We present a novel method for reconstructing a 3D implicit surface from a large-scale, sparse, and noisy point cloud. Our approach builds upon the recently introduced Neural Kernel Fields (NKF) representation. It enjoys similar generalization capabilities to NKF, while simultaneously addressing its main limitations: (a) We can scale to large scenes through compactly supported kernel functions, which enable the use of memory-efficient sparse linear solvers. (b) We are robust to noise, through a gradient fitting solve. (c) We minimize training requirements, enabling us to learn from any dataset of dense oriented points, and even mix training data consisting of objects and scenes at different scales. Our method is capable of reconstructing millions of points in a few seconds, and handling very large scenes in an out-of-core fashion. We achieve state-of-the-art results on reconstruction benchmarks consisting of single objects, indoor scenes and outdoor scenes.
LION: Latent Point Diffusion Models for 3D Shape Generation
Xiaohui Zeng, Arash Vahdat, Francis Williams, Zan Gojcic, Or Litany, Sanja Fidler, Karsten Kreis
NeurIPS 2022
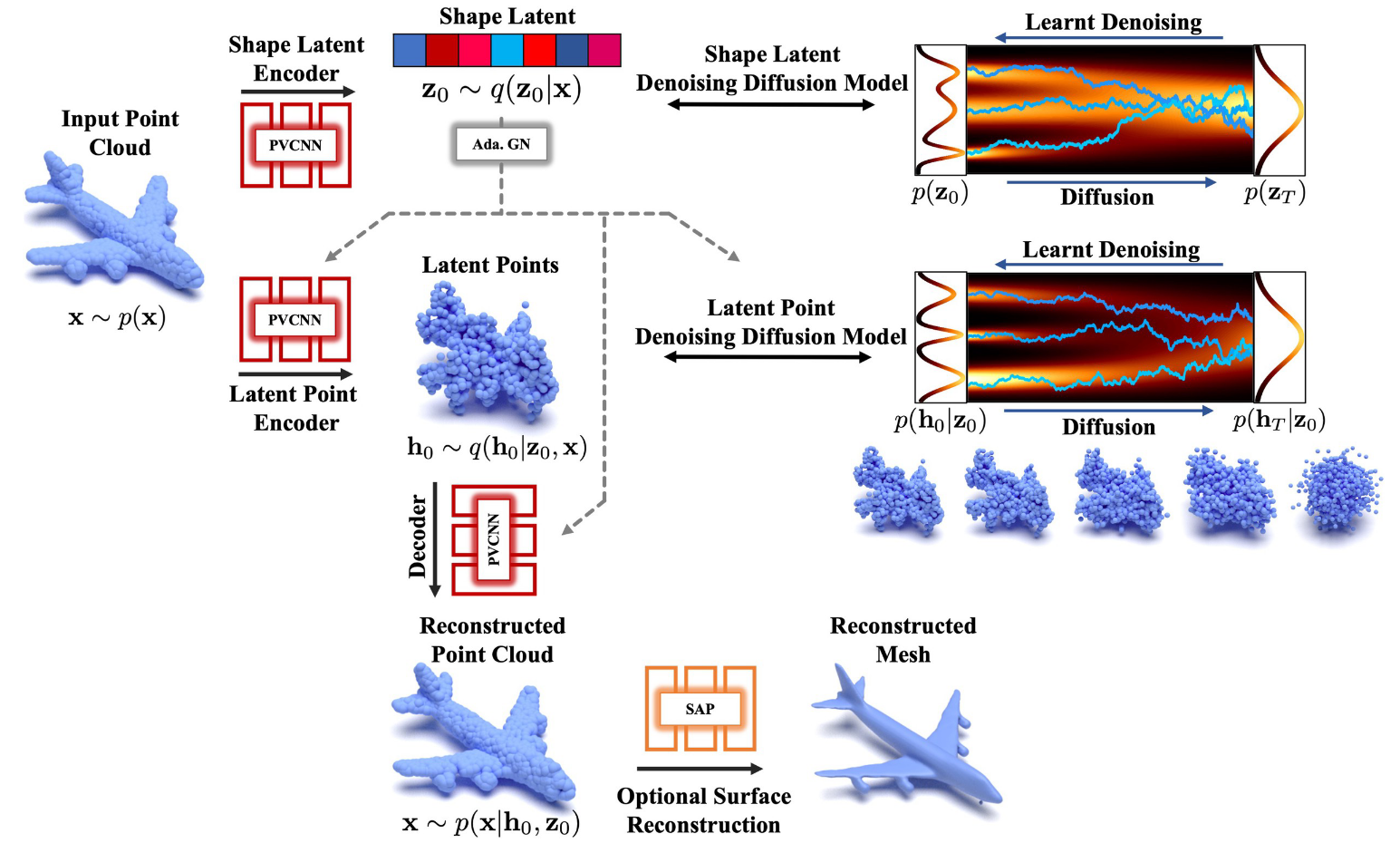
Denoising diffusion models (DDMs) have shown promising results in 3D point cloud synthesis. To advance 3D DDMs and make them useful for digital artists, we require (i) high generation quality, (ii) flexibility for manipulation and applications such as conditional synthesis and shape interpolation, and (iii) the ability to output smooth surfaces or meshes. To this end, we introduce the hierarchical Latent Point Diffusion Model (LION) for 3D shape generation. LION is set up as a variational autoencoder (VAE) with a hierarchical latent space that combines a global shape latent representation with a point-structured latent space. For generation, we train two hierarchical DDMs in these latent spaces. The hierarchical VAE approach boosts performance compared to DDMs that operate on point clouds directly, while the point-structured latents are still ideally suited for DDM-based modeling. Experimentally, LION achieves state-of-the-art generation performance on multiple ShapeNet benchmarks. Furthermore, our VAE framework allows us to easily use LION for different relevant tasks: LION excels at multimodal shape denoising and voxel-conditioned synthesis, and it can be adapted for text- and image-driven 3D generation. We also demonstrate shape autoencoding and latent shape interpolation, and we augment LION with modern surface reconstruction techniques to generate smooth 3D meshes. We hope that LION provides a powerful tool for artists working with 3D shapes due to its high-quality generation, flexibility, and surface reconstruction.
Learning Smooth Neural Functions via Lipschitz Regularization
Hsueh-Ti Derek Liu, Francis Williams, Alec Jacobson, Sanja Fidler, Or Litany
SIGGRAPH 2022
Neural implicit fields have recently emerged as a useful representation for 3D shapes. These fields are commonly represented as neural networks which map latent descriptors and 3D coordinates to implicit function values. The latent descriptor of a neural field acts as a deformation handle for the 3D shape it represents. Thus, smoothness with respect to this descriptor is paramount for performing shape-editing operations. In this work, we introduce a novel regularization designed to encourage smooth latent spaces in neural fields by penalizing the upper bound on the field’s Lipschitz constant. Compared with prior Lipschitz regularized networks, ours is computationally fast, can be implemented in four lines of code, and requires minimal hyperparameter tuning for geometric applications. We demonstrate the effectiveness of our approach on shape interpolation and extrapolation as well as partial shape reconstruction from 3D point clouds, showing both qualitative and quantitative improvements over existing state-of-the-art and non-regularized baselines.
Neural Fields as Learnable Kernels for 3D Reconstruction
Francis Williams, Zan Gojcic, Sameh Khamis, Denis Zorin, Joan Bruna, Sanja Fidler, Or Litany
CVPR 2022
We present Neural Kernel Fields: a novel method for reconstructing implicit 3D shapes based on a learned kernel ridge regression. Our technique achieves state-of-the-art results when reconstructing 3D objects and large scenes from sparse oriented points, and can reconstruct shape categories outside the training set with almost no drop in accuracy. The core insight of our approach is that kernel methods are extremely effective for reconstructing shapes when the chosen kernel has an appropriate inductive bias. We thus factor the problem of shape reconstruction into two parts: (1) a backbone neural network which learns kernel parameters from data, and (2) a kernel ridge regression that fits the input points on-the-fly by solving a simple positive definite linear system using the learned kernel. As a result of this factorization, our reconstruction gains the benefits of data- driven methods under sparse point density while maintaining interpolatory behavior, which converges to the ground truth shape as input sampling density increases. Our experiments demonstrate a strong generalization capability to objects outside the train-set category and scanned scenes.
Symmetry Breaking in Symmetric Tensor Decomposition
Yossi Arjevani, Joan Bruna, Michael Field, Joe Kileel, Matthew Trager, Francis Williams
arXiv preprint 2021
In this note, we consider the optimization problem associated with computing the rank decomposition of a symmetric tensor. We show that, in a well-defined sense, minima in this highly nonconvex optimization problem break the symmetry of the target tensor – but not too much. This phenomenon of symmetry breaking applies to various choices of tensor norms, and makes it possible to study the optimization landscape using a set of recently-developed symmetry-based analytical tools. The fact that the objective function under consideration is a multivariate polynomial allows us to apply symbolic methods from computational algebra to obtain more refined information on the symmetry breaking phenomenon.
Neural Splines: Fitting 3D Surfaces with Infinitely-Wide Neural Networks
Francis Williams, Matthew Trager, Joan Bruna, Denis Zorin
CVPR 2021 - Oral
We present Neural Splines, a technique for 3D surface reconstruction that is based on random feature kernels arising from infinitely-wide shallow ReLU networks. Our method achieves state-of-the-art results, outperforming Screened Poisson Surface Reconstruction and modern neural network based techniques. Because our approach is based on a simple kernel formulation, it is fast to run and easy to analyze. We provide explicit analytical expressions for our kernel and argue that our formulation can be seen as a generalization of cubic spline interpolation to higher dimensions. In particular, the RKHS norm associated with our kernel biases toward smooth interpolants. Finally, we formulate Screened Poisson Surface Reconstruction as a kernel method and derive an analytic expression for its norm in the corresponding RKHS.
VoronoiNet: General Functional Approximators with Local Support
Francis Williams, Daniele Panozzo, Kwang Moo Yi, Andrea Tagliasacchi
CVPR 2020 Workshop on Learning 3D Generative Models
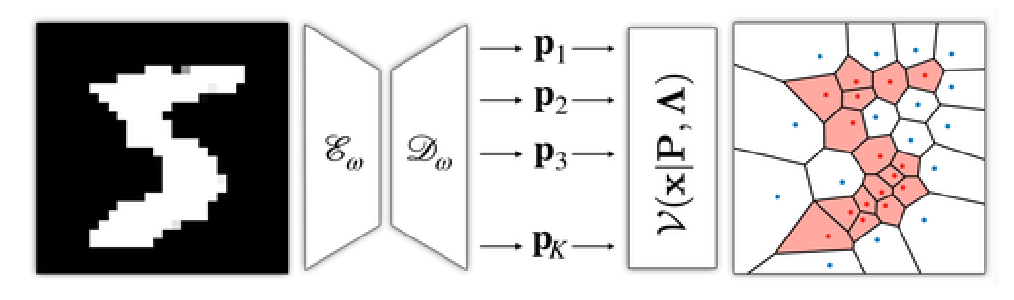
Voronoi diagrams are highly compact representations that are used in various Graphics applications. In this work, we show how to embed a differentiable version of it – via a novel deep architecture – into a generative deep network. By doing so, we achieve a highly compact latent embedding that is able to provide much more detailed reconstructions, both in 2D and 3D, for various shapes. In this tech report, we introduce our representation and present a set of preliminary results comparing it with recently proposed implicit occupancy networks.
Gradient Dynamics of Shallow Univariate ReLU Networks
Francis Williams, Matthew Trager, Claudio Silva, Daniele Panozzo, Denis Zorin, Joan Bruna
NeurIPS 2019
We present a theoretical and empirical study of the gradient dynamics of overparameterized shallow ReLU networks with one-dimensional input, solving least-squares interpolation. We show that the gradient dynamics of such networks are determined by the gradient flow in a non-redundant parameterization of the network function. We examine the principal qualitative features of this gradient flow. In particular, we determine conditions for two learning regimes:kernel and adaptive, which depend both on the relative magnitude of initialization of weights in different layers and the asymptotic behavior of initialization coefficients in the limit of large network widths. We show that learning in the kernel regime yields smooth interpolants, minimizing curvature, and reduces to cubic splines for uniform initializations. Learning in the adaptive regime favors instead linear splines, where knots cluster adaptively at the sample points.
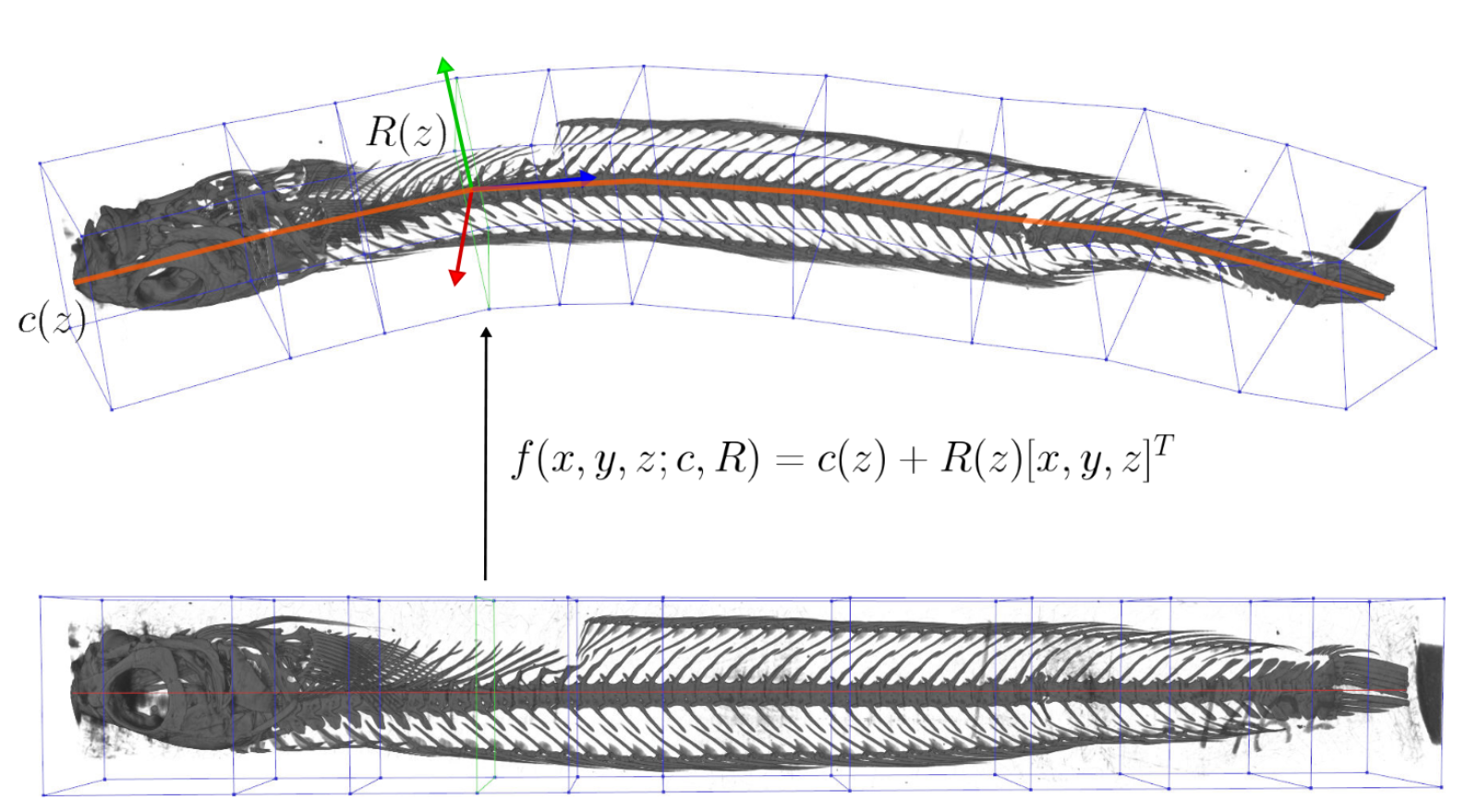
Unwind: Interactive Fish Straightening
Francis Williams, Alexander Bock, Harish Doraiswamy, Cassandra Donatelli, Kayla Hall, Adam Summers, Daniele Panozzo, Cláudio T. Silva
CHI 2020
The ScanAllFish project is a large-scale effort to scan all the world’s 33,100 known species of fishes. It has already generated thousands of volumetric CT scans of fish species which are available on open access platforms such as the Open Science Framework. To achieve a scanning rate required for a project of this magnitude, many specimens are grouped together into a single tube and scanned all at once. The resulting data contain many fish which are often bent and twisted to fit into the scanner. Our system, Unwind, is a novel interactive visualization and processing tool which extracts, unbends, and untwists volumetric images of fish with minimal user interaction. Our approach enables scientists to interactively unwarp these volumes to remove the undesired torque and bending using a piecewise-linear skeleton extracted by averaging isosurfaces of a harmonic function connecting the head and tail of each fish. The result is a volumetric dataset of a individual, straight fish in a canonical pose defined by the marine biologist expert user. We have developed Unwind in collaboration with a team of marine biologists: Our system has been deployed in their labs, and is presently being used for dataset construction, biomechanical analysis, and the generation of figures for scientific publication.
Deep Geometric Prior for Surface Reconstruction
Francis Williams, Teseo Schneider, Cláudio T. Silva, Denis Zorin, Joan Bruna, Daniele Panozzo
CVPR 2019
The reconstruction of a discrete surface from a point cloud is a fundamental geometry processing problem that has been studied for decades, with many methods developed. We propose the use of a deep neural network as a geometric prior for surface reconstruction. Specifically, we overfit a neural network representing a local chart parameterization to part of an input point cloud using the Wasserstein distance as a measure of approximation. By jointly fitting many such networks to overlapping parts of the point cloud, while enforcing a consistency condition, we compute a manifold atlas. By sampling this atlas, we can produce a dense reconstruction of the surface approximating the input cloud. The entire procedure does not require any training data or explicit regularization, yet, we show that it is able to perform remarkably well: not introducing typical overfitting artifacts, and approximating sharp features closely at the same time. We experimentally show that this geometric prior produces good results for both man-made objects containing sharp features and smoother organic objects, as well as noisy inputs. We compare our method with a number of well-known reconstruction methods on a standard surface reconstruction benchmark.
ABC: A Big CAD Model Dataset For Geometric Deep Learning
Sebastian Koch, Albert Matveev, Zhongshi Jiang, Francis Williams, Alexey Artemov, Evgeny Burnaev, Marc Alexa, Denis Zorin, Daniele Panozzo
CVPR 2019
We introduce ABC-Dataset, a collection of one million Computer-Aided Design (CAD) models for research of geometric deep learning methods and applications. Each model is a collection of explicitly parametrized curves and surfaces, providing ground truth for differential quantities, patch segmentation, geometric feature detection, and shape reconstruction. Sampling the parametric descriptions of surfaces and curves allows generating data in different formats and resolutions, enabling fair comparisons for a wide range of geometric learning algorithms. As a use case for our dataset, we perform a large-scale benchmark for estimation of surface normals, comparing existing data driven methods and evaluating their performance against both the ground truth and traditional normal estimation methods.